Nuke Olaf - Log Store
역삼각함수 정리 - 아크사인, 아크코사인, 아크탄젠트 본문
역삼각함수에 대해 이해하기 위해서는 우선 역함수의 개념에 대해 정확히 인지하고 있어야 한다. 역삼각함수 또한 삼각함수의 역함수이기 때문이다.
1. 역함수란?
어떤 함수 $f(x)$ 에서 정의역과 치역이 일대일 대응인 경우 역함수가 존재한다.
역함수에서는 정의역과 치역이 바뀌게 된다.
$f:X \rightarrow Y$ 일대일 대응 $\Rightarrow$ $f$의 역함수 $f^{-1}:Y \rightarrow X$ 존재
- $f(f^{-1}(x))=x,\quad x\in Y$ → 합성시키면 자기 자신이 나온다.
위의 역함수 $f^{-1}(x)$ 의 정의역에 들어가는 원소 $x$ 는 $Y$의 원소이다.
- $f^{-1}(f(x))=x,\quad x\in X$ → 합성시키면 자기 자신이 나온다.
위의 함수 $f(x)$ 의 정의역에 들어가는 원소 $x$ 는 $X$의 원소이다.
2. 역삼각함수란?
역삼각함수는 $f^{-1}(x)$에서 $f$자리에 $\sin$ , $\cos$ 또는 $\tan$ 를 위치시키는 것이라고 이해하자.
그런데, 삼각함수는 정의역과 치역 사이의 관계식을 만들 수 없는 함수이다. 그러므로 삼각함수의 역함수 값을 구하기 위해 $f$의 대응을 살펴보아야 한다.
**관계식을 만들 수 있는 함수의 경우, 예를 들어 $f(x)=x+2$ 의 경우를 생각해보자. 이때 $f(x)$ 의 역함수를 $f^{-1}(x)=x-2$ 라고 관계식으로 정의할 수 있다.
**그러나 아래와 같이 관계식을 만들 수는 없지만, 일대일 대응이 되는 함수 $f$에 대해서는, $f^{-1}(0)$의 값을 알기 위해서는 $f(x)$에서 $x$에 어떤 값이 들어가야 $0$이 되는지를 살펴봐야 한다.
아래의 예에서 $f(a)=0$ 이므로, $f^{-1}(0)=a$ 즉, $f$의 역함수의 값을 알 수 있다.
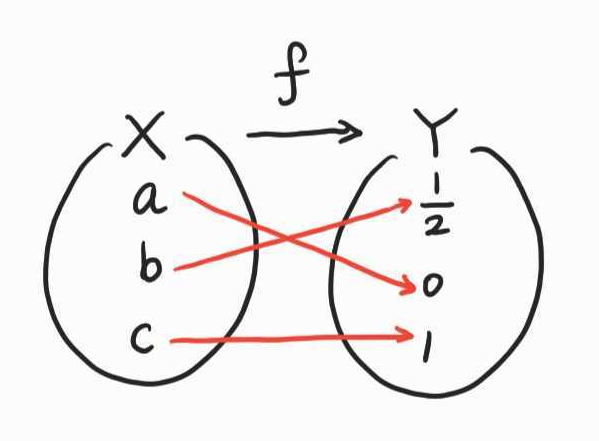
** 삼각함수는 일대일 대응이 아니다. ex) $\sin \frac{\pi}{6}=\sin \frac{5}{6}\pi$ → 다른 두 정의역 값이 하나의 치역을 가리킴
그래서 삼각함수의 역함수를 구할때, 삼각함수가 $x$ 값 하나에 대해서 $y$ 값 하나에만 일대일 대응이 되는 부분으로 정의역을 제한한다.
** 그래서 역삼각함수의 정의역과 치역에 대해 정확히 알고 있는 것이 중요하다
- 삼각함수에서 일대일 되는 정의역을 찾을 때 조건
- $0\in X$ → 정의역에 0 이 포함되어야 한다.
- $Y = [-1, 1]$ → 치역은 일대일 대응이 되는 원래의 치역 $(-1\leq Y\leq1)$
*$[\quad]$ 는 닫힌구간을 의미한다.
2 - (1). 역사인함수 (\arcsin x)
$\sin : [-\frac{\pi}{2},\frac{\pi}{2}] \rightarrow [-1,1]$ 일대일 대응
$\Rightarrow$ $\sin^{-1}:[-1,1]\rightarrow [-\frac{\pi}{2},\frac{\pi}{2}]$ 역사인 함수
$\Rightarrow$ $y=\sin^{-1}x$
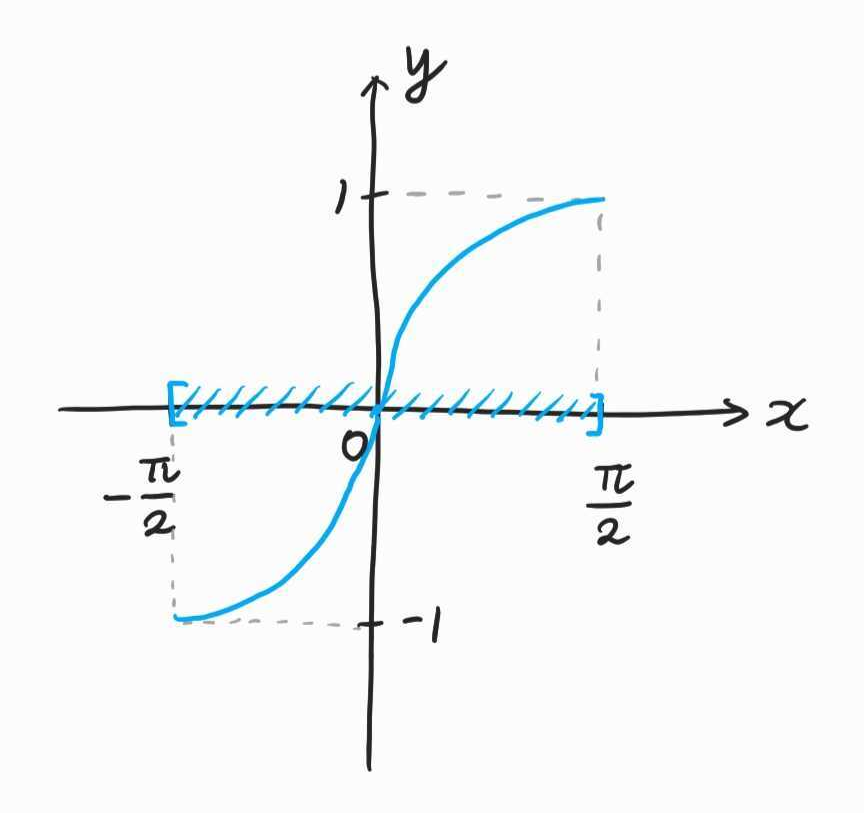
$$\sin(\sin^{-1}(x))=x,x\in[-1,1],\quad \sin^{-1}(\sin(x))=x,x\in[-\frac{\pi}{2},\frac{\pi}{2}]$$
예제)

2 - (2). 역코사인 함수 (\arccos x)
$\cos : [0,\pi] \rightarrow [-1,1]$ 일대일 대응
$\Rightarrow$ $\cos^{-1}:[-1,1]\rightarrow [0,\pi]$ 역코사인 함수
$\Rightarrow$ $y=\cos^{-1}x$

$$\cos(\cos^{-1}(x))=x,x\in[-1,1],\quad \cos^{-1}(\cos(x))=x,x\in[0,\pi]$$
**역코사인 함수의 치역은 양수이다. 즉, 역코사인의 값은 음수가 없다는 사실을 기억하자.
예제)

2 - (3). 역탄젠트 함수 (\arctan x)
$\tan : (-\frac{\pi}{2},\frac{\pi}{2}) \rightarrow (-\infty,\infty)$ 일대일 대응
$\Rightarrow$ $\tan^{-1}:(-\infty,\infty) \rightarrow (-\frac{\pi}{2},\frac{\pi}{2})$ 역탄젠트 함수
$\Rightarrow$ $y=\tan^{-1}x$
*$(\quad)$ 는 열린구간을 의미한다. 점근선에 해당하는 값은 포함되지 않는다.
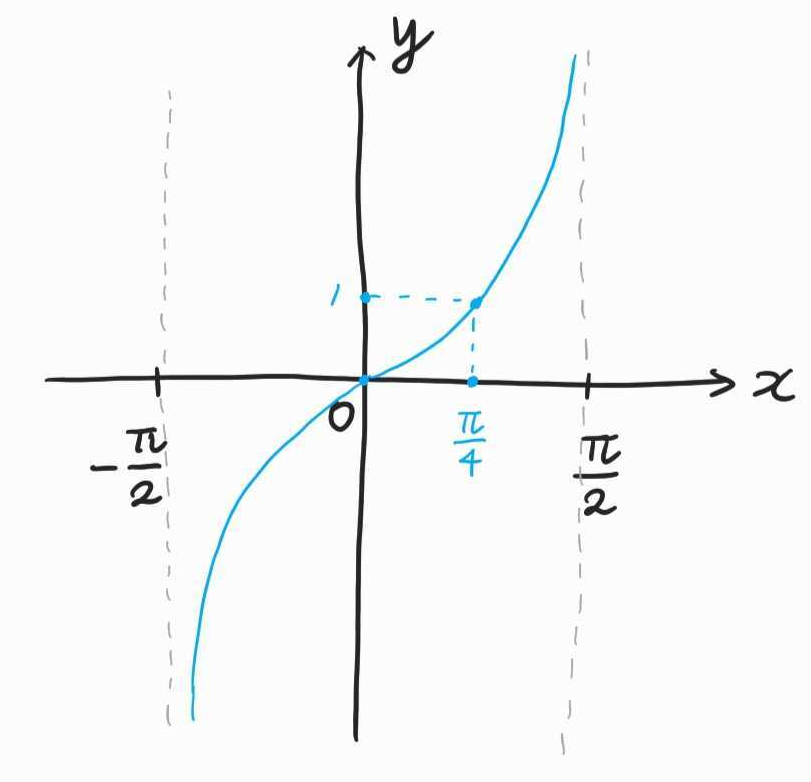
$$\tan^{-1}(0)=0, \quad \tan^{-1}(1)=\frac{\pi}{4}$$
역탄젠트에서는 위의 두 식을 가장 많이 사용한다. 역탄젠트에서는 역사인, 역코사인 처럼 대수적인 계산을 하는 문제가 나오지 않는다. 역탄젠트 $x$의 그래프의 개형을 알고 있는 것이 중요하다.

'Mathematics' 카테고리의 다른 글
| 연쇄율과 음함수 미분 (0) | 2020.10.14 |
|---|---|
| 도함수와 미분법 - 미분 공식 정리 (0) | 2020.10.14 |
| 함수와 그래프 (0) | 2020.05.10 |


